この記事は、文系で数学が苦手だけども入試で使わなければいけない人や、理系で数学がとても苦手な人たちに向けたものです。
受験生向けですが、普段、定期試験で点数が取れない人も、自分の点数が取れない原因がどこにあるのかを探るために一読をお勧めします。

原則:基礎計算/公式理解→計算/入試問題演習
君たちは基本的な計算が素早くできない
まず言っておきたいのが、数学が苦手だ、と言う人の中には、単純に計算が遅すぎて、数学の講義の内容や、公式の理解そのものに時間がかかりすぎて、練習ができずに定着せずそれがずっと続いているだけと言う人がかなりの数います。
そして、もう一つありがちなのが、そうした人は、自分の計算の遅さに気づいてすらいない、ということです。
このために、数学が苦手な人のほとんどは、計算演習を2週間ほど続けてもらい、内容理解や公式暗記のために必要な計算スピードを身に付けてもらいます。
公式もなんとなく覚えただけで、試験中に素早く使えるほど覚えてない
また、計算が問題ない人も、数学の公式そのものを素早く運用する練習はまだ未熟だという人が、数学が苦手な人の中には多いです。
まあ、ほとんどの人は、公式を覚えていても、ゆっくりにしか出てこない場合が多く、基礎計算も遅いし、公式が出てきても形があやふやで何となくしか覚えてないわ、そこからの計算がまた遅いしと言うような地獄絵図だったりします。
このため、基本的な計算に加えて、公式そのものの理解、そしてどの公式を使うかを素早く判断し、いかに早くその問題を解くかという、公式の運用も練習していく必要があります。

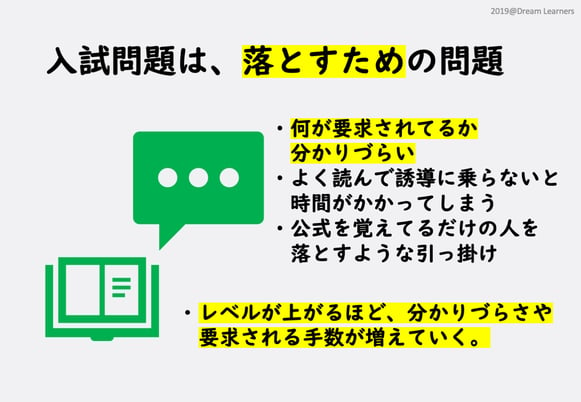
入試問題は落とすための問題なんだから、わかりやすく丁寧にどの公式を使うとか書いてあるわけがない
そして、君たちが1番勘違いしているのが、入試の問題と言うのは、選抜をするためのテストだ、ということです。定期テストのように、わかりやすく丁寧にどの公式を使うか書いてやるわけがありません。
模試を受けて、公式は知っていたのにできなかった、みたいな嘆き方をする人は、そういった仕組みが分かっていない、世間知らずのあまちゃんだと言うことです。
一方で、入試問題を使ってある問題集の中でも、実戦形式のフリをしながら、公式の使い方を理解させるためのわかりやすく編集した問題を多く用いているものがあります。
ですから、最初はそういった誘導がわかりやすい問題集を使いながら解法暗記をしていくのですが、最終的には、過去問であるとか、入試問題がそのまま載っているような、一見しただけでは何をして良いか分かりづらいレベルの、実践形式のものに取り掛かる必要があります。
虚無の時間をなくす(超重要)
また、数学の苦手な人にありがちな「何事もなしてない時間」「赤ペンのインクが減っているだけの時間」「目が滑っているだけの時間」「数学コンプレックスと戦っている精神と時の部屋」を減らすのも非常に重要です。
- 赤ペンで回答を写しているだけの時間
- 「次に自力でやる」ことを考えずに解説を読んでいる時間
- できない自分を受け入れられずに問題演習中に固まっているだけの時間
こうした虚無の時間をいかに減らすかが数学の学習を効果的に進めるかの鍵です。
君たちがどれだけ数学が苦手かと、君たちが希望する進路にどれだけ数学が必要かは、全く無関係です。数学コンプレックスと戦わずに、教科書と向き合ってください。まともに数学と向き合い、自分が受ける試験の、試験時間中に取るべき点数が取れるように練習しましょう。
基礎計算の練習(2週間で完了させる)
基礎計算に不安のある人は、小学5年レベルの計算ドリルをやり直しましょう。ただ、単なる計算だけのドリルよりも、考え方や注意すべきポイントを丁寧に掲載している、中学入試向けの基礎計算のドリルが良いでしょう。
1日20ページ程度、1週間で1冊、合計2週間で5年生、6年生のものを一通り終えてください。それでも心配ならば、2回目を1週間でやり直しても良いでしょう。
ここに時間をかける意味はあまりないです。できるだけ素早く計算練習は完了させてください。
公式理解→計算(文系全範囲)
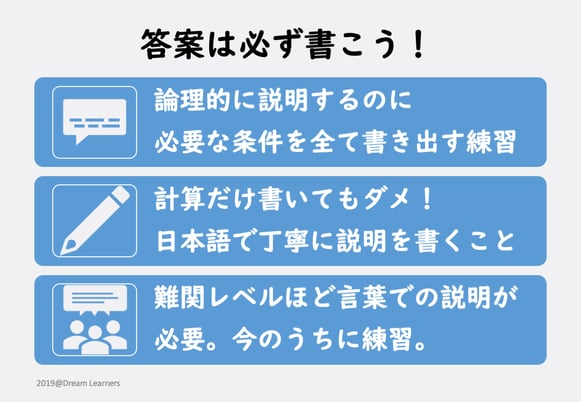
大前提:私大専願でも、記述答案を書きましょう
時々あるのですが、「答案を書いたほうがいいか」と言う質問です。
結論から言うと、必ず書いて下さい。
ただし、ただの計算の羅列になってはいけません。
「問題文に記載されている条件」「説明に必要な前提条件」「それらから立てられる式」「導かれる結論」など、答案を書くのは、こうした論理的に説明する上で必要なことを必ず書き出して説明する練習です。これをやらないと、どれだけ問題演習をしても、どこがわからないのかわからないまま、何も成長せずに終わります。
学校ではノートに答案を書いて提出するといった課題の出し方がポピュラーだと思いますが、ただの計算ノートになっているだけの人が多いです。どういう意図で、どういう公式を使って、どういう考え方でそのような立式をしたのか、など、書きましょう。計算の練習をする問題ならばそれでいいのですが、証明問題までそうなっていては、何のための問題演習だかわかりません。
難関レベルになってくればくるほど、私大でも記述答案を要求されて、日本語で丁寧に説明しなければ有効な答案にならないことが多くなってきます。取り扱っている問題が基礎的なもののうちから、論理的に答案を書くよう習慣づけてください。
公式理解・公式計算練習の問題集の紹介
ベストな教材は「教科書」です。練習問題を、自力(問題のみを提示された状態)で答案を書いて解法を明確にした上で解けるようにすることが基礎力養成になります。
とは言っても、教科書をやって、と言ってもやってくれない人が多いので、問題集を紹介します。教科書をやれる人は、絶対に教科書が良い、ということを念押ししておきます。ちゃんと読んでみてください。
まず、計算にあまり問題がなく、公式理解とその練習をしたいと言う生徒向けの教材を紹介します。実教出版の「短期集中ゼミ」シリーズです。自信がない人は「Express」から始めてください。2BCも同様にあります。
計算スピードを「問題」を使ってつけたい場合は、上記の教材をやった前提ですが、以下のような「数学の問題」を解くための手順としての計算を早めるものを推奨します。
入試問題演習(目標:私大標準〜地方国公立レベル)
ここまで到達して、数学の学習法を読む
このレベルまで到達してから、数学の学習法の本を読んでください。どうしてこのレベルにならないと読んではいけないかと言うと、そもそも計算が遅い公式が頭に入っていないと言う段階では、結局勉強法の本を読んだところで、そこをやり直せと言われるのがオチだからです。
以下に紹介する志田先生の「数学の勉強法をはじめからていねいに」を読みながら、各分野の特徴を掴んで、解法暗記のやり方を工夫して進めてください。
解法暗記の考え方
「初見の問題を、自分で解答を出せるまで考えなさい」と言う指導を受けたことのある高校生はおそらく多いと思います。こういった指導は、はっきり言ってしまえば、数学に時間をかけさせて、生徒たちを学校に縛り付けるための方便としか思いません。
確かに、超難関大学など、その場で考える力が必要な大学を目指しているのであれば、こうした訓練は必要でしょうけど。ほとんどの高校生にとっては、基本的な問題へのアプローチすら頭に入っていないことが多いでしょう。
まずは、典型的で基本的な解法を頭に入れていくことが、数学の勉強では必要です。考える材料がなければ、そもそも、問題文を見たところで何も考えることはできません。
私は、5分程度考えても、鉛筆やシャープペンシルがピクリとも動かないのであれば、まず解説の冒頭の数行だけ読んで、何をしたらいいかわかればまた自力で書いてみる、読んでもまた5分ぐらい動きが止まるようであれば、それはレベルが合ってないと思って、何をわかっていればよかったかという意味で解答を理解して暗記する勉強に切り替える、というやり方で、何もわからない問題は10分程度で切り上げて、解法暗記に移るようにしていました。
もちろん、一度で覚え切れるわけはありませんから、そうして頭に入れた解法を、その日の夜などに改めて確認する、といったことをやっていました。また、解法暗記が進めば、問題文を読んですぐに解答が浮かんでくるようになりますから、復習や確認の時間が格段に少なくなり、効率が上がります。
解法暗記と言っても、どれぐらい覚えなくてはいけないのか、心配な人もいると思います。
しかし、答案の書き方は、そこまで自由度が高いわけではありませんから、文系数学全体で、まずは入試問題150問程度の解法暗記ができれば、次のレベルに上がっていくことができるでしょう。もしあなたが高校1年生で、これからも授業と並行して解法暗記のチャンスがあるなら、チャート式やFocusGoldなどで数百問の入試問題解法を暗記することをお勧めします。

具体的な演習材料
解法暗記用:教科書レベルを徹底せよ
教科書の節末問題・章末問題(巻末に簡素な解答があるもの)を、解法暗記用(問題文での要求把握+答案作成パターン暗記)の問題集として利用します。教科書には、それらの問題を解くために必要なことが全て書いてあります。教科書よりも、解説が詳しいものが好みであるならば、「マセマ 元気に伸びる数学 問題集」シリーズが良いでしょう。
私大標準(有名大レベル未満や、地方都市トップ私立)であれば、ここまでの問題集+10年分の繰り返し過去問演習で十分戦えるでしょう。
教科書?馬鹿にすんな、とか思いました?
それは誤解です。数学がチンプンカンプンという受験生のほとんどは、教科書レベルのことが必ずといっていいほどできていませんし、問題集ばかり見ていて、肝心の教科書に入試問題の基本レベルに当たる問題が掲載されていることすら気づいていません。
馬鹿にしているわけではなく、馬鹿正直に、必要なことを提案しているだけです。
実戦演習(落とすポイントを見抜く)用
地方国公立レベルであれば、もう1段階上のレベルの問題集まで仕上げておくのが良いでしょう。そのレベルになってくると、ある程度勉強ができる受験生が受けてくるとわかっていますから、彼ら彼女らを落とすための問題設計になっており、わかりやすく公式を誘導してくれるような問題はかなり少なくなってきます。
そのため、問題の解説を読むのにも、かなり頭を使って読んで理解していかなければならないレベルになっています。
簡素に核心だけをまとめてあり、頭を使わせてくるのは「松田の数学1A2B典型問題type100」。私は、個人的には、type100の説明で、核心的な理解を頭に入れておくことをオススメします。基本的には自分の性格と実力に合わせて選んでください。
TYPE100は旧課程用の問題集のため、「整数問題」が入っていますが飛ばしてください。「確率統計」については扱っていません。
ここでも、インプット用に教科書を用意して、必要に応じて参照することを忘れないでください。
まとめ
以上のように、数学の入門レベルの学習は、
- 基礎計算の練習
- 公式の確認・公式運用の練習
- 入試問題演習
の手順で進めてください。


